令和４年度入試の受験生は要注意！！四分位数と箱ひげ図ってなに？

愛知県公立高校入試情報に強い小牧市の個別指導学習塾
名学館小牧新町校　塾長の吉澤です。

２０２１年度から教科書が新しく変わりましたね。
その際に例えば、新しい中学２年数学の教科書にある
『箱ひげ図とデータの活用』
の範囲は、現在の中３が中２時代の教科書には載っていなかったので小冊子で移行措置対応をしたかと思います。

というわけで、教科書に載っていないし、追加事項なので入試にはとても狙われやすい単元だと思っています。

今日は『四分位数』と『箱ひげ図』について簡単におさらいしてみましょう！！

四分位数ってなに？四分位範囲ってなに？

データを大きさの順（小さい順）に並べたときに、４等分する位置にくる３つの値を
四分位数
といいます。

四分位数は、小さい方から順に
・第１四分位数
・第２四分位数（中央値）
・第３四分位数
と言います。

まずはデータの個数が奇数個の場合から見ていきましょう。

奇数個の場合の四分位数について

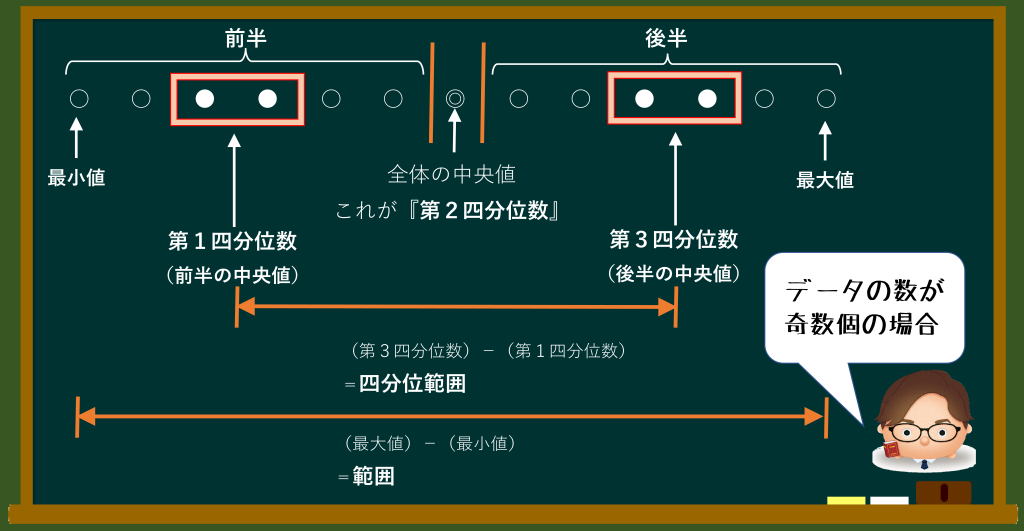
まずはデータを小さい順に並べ替えます！！

上の例の場合データ個数は、１３個あるので
中央値は７番目のデータになり、この値がそのまま
『第２四分位数』
になります。

次に『第１、３四分位数』を求めるためにデータを前半と後半に分けますが、真ん中のデータは含まれないことに注意してください！！

『第１四分位数』は、前半のデータ６個の中央値になるので、
３番目と４番目の平均値になります。

同様に
『第３四分位数』は、後半のデータ６個の中央値になるので、
１０番目と１１番目の平均値になります。

偶数個の場合の四分位数について

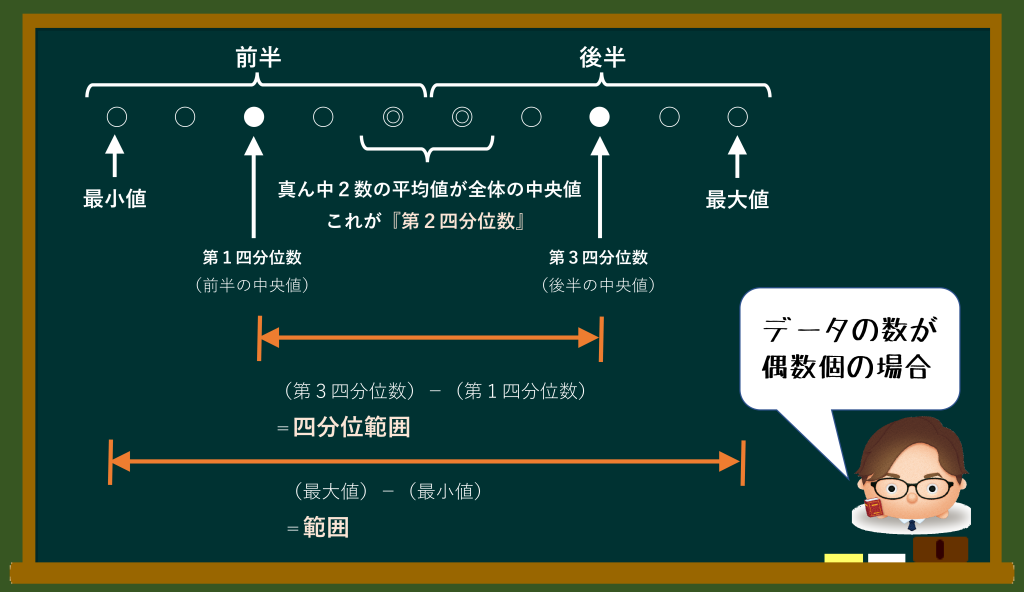
データ個数が偶数個の場合は、中央値が真ん中２数の平均になる。
このとき、データはちょうど前半と後半わけることができるから、奇数個の場合よりはわかりやすいと思います。

四分位数の出し方は自体は、奇数個の場合と同じです！！

箱ひげ図を描いてみよう

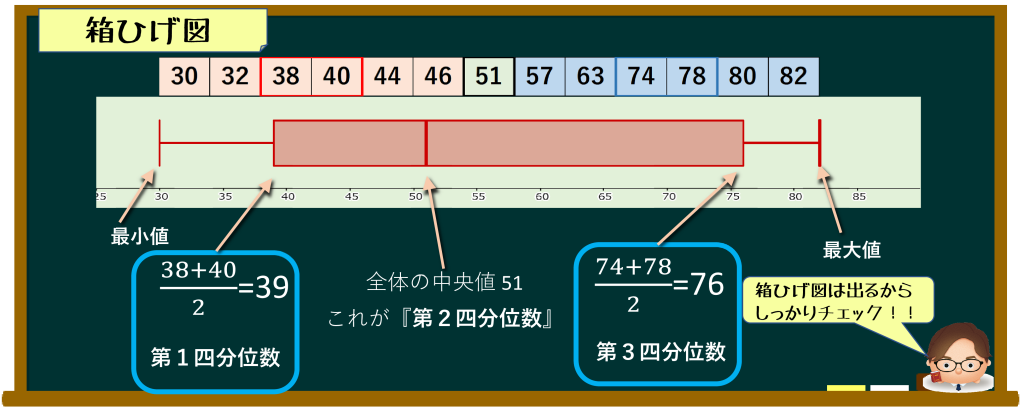
それでは、例としてデータが奇数個の場合の箱ひげ図を描いてみました。